s u n p e n d u l u m

s t a t i o n F / g e o m e t r y

by Hofstetter Kurt, 2001

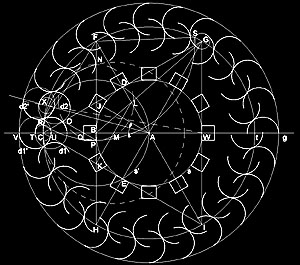The geometry of interpenetration - achieved by 2 circles, which are translated parallel by their radii - formulates a specific transition between inner and outer space; outside turns inside and inside outside *1). 24 pairs of half-cylindrical panels, translated by the radii of their semi-circular cross sections towards the center, are setup in a circle and form the entries from all directions. The requirement to optimize the light situation in the pavilion for the screens yields the premise: “No direct light beam is allowed to enter the inner space“. Therefore the adjacent panels have to touch each other. The optimization of their semi-circular cross sections is directly derived from the principle of the Golden Section and can easily be constructed by only using a set of compasses and a ruler:

Let A be the mid-point of the pavilion, g the base line through A. The circle s with center A is translated parallel by its radius AB towards B and yields the circle s’ with radius BC (interpenetration s, s’); s intersects s’ at D and E; the circle t with radius AC intersects the line through AD at F and I, the line through AE at G and H; CGI is a equilateral triangle with inscribed circle s and circumscribed circle t. FH intersects CG at J and CI at K; From JC=JF=JA=JK=KC=KH=KA results: CKJ is a equilateral triangle with height BC. BG intersects AF at L and LK intersects AB at M. The arc with mid-point M and radius MC intersects FH at N; the arc with center J and radius JN intersects FH at P and CD at O;
KJ is major and JN is minor of KN *2); PJ=JN, hence JP is major and PK minor of JK; JP=JO and JK=JC, hence JO is major and OC minor of JC; OP intersects AC at Q, OP is parallel to JA, according to the intercept theorem AQ is major and QC minor of AC; the arc with mid-point F and radius FP intersects at R and S. The circle with radius CR intersects g at T and U; TU is the radius of the interpenetrating circles d1 and d1’. Rotating the pair of circles (d1, d1’) by 15 degrees around the mid-point A yields the pairs of circles (d2, d2’), whereby the circles d1 and d2’ as well as d2 and d1’ touch each other. A circle with 24 touching, interpenetrating pairs of circles is iteratively completed, whereby their semi-circles form the optimized cross sections of the half-cylindrical pairs of panels.

* AV is the outer radius of the pavilion. BQ is the depth and BP half the length of the monitor case.

To experience the discrete circle of 12 monitors, directed towards the center, in an intimate space, the distance between two opposite screens has been fixed at 6 m, i.e. AB = 3m. According to the Golden Section, described above, the optimal diameter of the pavilion is 14,70 m and the width of each monitor case 82 cm; the line through XW defines the exact length of the half-cylindrical panels by intersecting the interpenetrating circles d2 and d2’, resulting an adequate width for the entries (111cm on the outside, 80cm on the inside).

*1) see Paul Klee, “Zur räumlich körperlichen Durchdringung“
*2) see Georg Odom, “Construction of the Golden Section“ (1982)