s u n p e n d u l u m

p a v i l i o n # 1 / g e o m e t r y

by Reinhard Haslwanter and Hofstetter Kurt, 1999

model 1:20 by Reinhard Haslwanter, video still by Barbara Doser

The geometry of the spiral as spatial translation and rotation - respectively parallelism and circulation - formulates a specific transition between inner and outer space. The construction principle of this spiral is based on the Golden Section, which by itself results from the light of the sun and the rotation of the earth. Through iterative use of this principle, beginning with a single unit of 1 cm, it is possible to derive all dimensions using only a set of compasses and a ruler. After 14 iterations the resulting dimension is 843 cm, which is the diameter of the circle of the 12 supporting pillars.

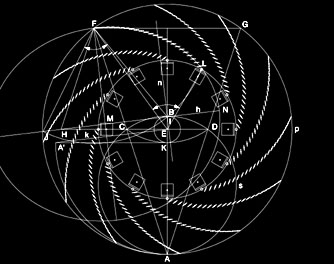
Let s be a circle with the diameter AB = 843 cm. A Golden Triangle ACD is inscribed in this circle. The height AE of this Golden Triangle is the outer radius of the pavilion. E is the resulting mid-point of the pavilion and thus the centre of the pillar-ring. Into the outer circle another Golden Triangle AFG is constructed. The corner F marks the starting point of an arc of lamellas, generated by an ellipse. The geometry of the ellipse as planar translation and rotation - respectively parallelism and circulation - can again be constructed according to the Golden Section:

the vertex of the minor half-axis is F;
the major axis of the ellipse is constructed from point H and slope k:
   one point H of the major axis results from a Golden Triangle CFH with 1 corner at F,
   the slope k results from k = BE / (AE-BE) = EK / AK = EK / A’K;
the foci I, J on the major axis h:
   a normal n to the major axis h that goes through B is chosen,
   the focus I is the intersection of n and h;
   the focus J results from the equivalent length of FI and FJ;

* the chord length of the arc of lamellas is FI ( = distance F to pillar L)
* the focal constant of the ellipse is the radius of the pavilion AE (distance of the foci IJ)
* the angle < JFI is equivalent to the angle < FEL
* let MN be the major half-axis of the ellipse thus the relation of MI to IN is equal to the relation of MN to FM

In the closed position the lamellas are oriented parallel to the major axis of the ellipse. Each arc of lamellas is tangential to the chord of the following one – no light beam can directly reach the space inside the ring of pillars. In the opened position the lamellas are parallel to the minor axis. Thus a maximum of transparency is achieved – the light of the screens streams outside in an ideal way.